S Matrix from Matrix Product States
Category: Scientific HighlightsPublished in Physical Review Letters
ABSTRACT:
We use the matrix product state formalism to construct stationary scattering states of elementary excitations in generic one-dimensional quantum lattice systems. Our method is applied to the spin-1 Heisenberg antiferromagnet, for which we calculate the full magnon-magnon <nobr>S</nobr> matrix for arbitrary momenta and spin, the two-particle contribution to the spectral function, and higher order corrections to the magnetization curve. As our method provides an accurate microscopic representation of the interaction between elementary excitations, we envisage the description of low-energy dynamics of one-dimensional spin chains in terms of these particlelike excitations.
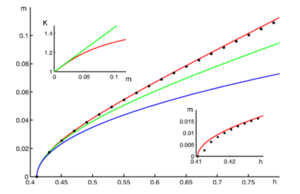
| Figure: The magnetization m versus applied magnetic field h for the spin-1 Heisenberg chain. Our results (red, upper curve) with bond dimension D ¼ 64 are compared to the hard-core boson square-root dependence (blue, lower curve) and first order corrections by the scattering length a2 (green, middle curve). The direct MPS calculations (black dots) were done at the same bond dimension of D ¼ 64. The bottomright inset provides a close-up of the phase transition. The top-left inset provides our result for the LL parameter K in function of the magnetization m (red), compared to the linear relation based on the scattering length (green). | ||
|---|---|---|---|
Vanderstraeten L., Haegeman J., Osborne T.J., Verstraete F. (2014), S Matrix from Matrix Product States, Phys. Rev. Lett. 112, 257202. DOI:10.1103/PhysRevLett.112.257202
Other Recent ViCoM Publications
Sensengasse 8/12
A-1090 Vienna
AUSTRIA
T: +43-1-4277-51401
F: +43-1-4277-9514